X SCIENCE PRACTICE PAPER SA I [4]

SECTION - A

Question numbers 1 to 10 are  of one  mark  each.

1.           According to Euclid’s  division algorithms HCF  of any  two  positive integers a and  b with a > b is obtained by applying Euclid’s  division lemma  to a and  b to find  q and  r such  that a bq  r where  r must  satisfy.

(A)    1 < r < b               (B)    0 < r < b               (C)   0 ≤     r < b              (D)    0 < r  ≤   b

2.           In figure  1, the graph of a polynomial p(x) is shown.  The number of zeroes  of p(x) is :

 (A)    3                            (B)    4                            (C)    1                            (D)    2

3.           In figure  2, if DE || BC then  x equals  to :

(A)    3 cm                                   (B)    4 cm             (C)    7 cm                             (D)    4.7 cm

4.           If sin 2 A = cos(A - 6°) where   2A  and  (A - 6°) are both  acute  angles  then  the vlaue  of A is :

(A)    16°                      (B)    32°                (C)    48°                (D)    45°

5.           Given  that  cosA = 1/2the value  of  2sec A /(1 + tan ² A) is :

(A)    1                         (B)    2                    (C) 1/2                   (D)    0

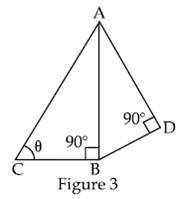
6.           In figure  3, AD=3cm, BD=4cm and  CB=12 cm them  tan A equals  :

 (A) 3 / 4                     (B) 5 /12                               (C) 4/ 3                                  (D)      5 /12

7.           The decimal expansion of  141 will terminate after  how  many  places  of decimals ?

(A)    1                         (B)    2                                    (C)    3                                    (D)    will not terminate

8.           The pair  of linear  equations 7x 3y=4  and  14x  4y=5  have  :

(A) One Solution       (B) many solution              (C)    many  solutions         (D)    no solution

9.           If sec A=cosec B= 12 then  A    B is equal  to :

(A)    zero                   (B)    >90°                             (C)    90°                                (D)    <90°

10.       For a given data  with 50 observations the ‘less than  ogive’ and the ‘more then ogive’ intersect at(15.5, 20).  The median of the data  is :

(A)    4.5                      (B)    2 0                                (C)    5 0                                 (D)    15.5

SECTION - B

Question numbers 11 to 18 carry  2 marks each.

11.       Is 7  x  11 x  13+13 a composite number ?  Justify your answer.

12.       Can  (x - 3) be the  remainder on the  division of a polynomial p(x) by (2x+5) ?  Justify  your answer.

13.       In figure  4, ABCD is a rectangle. Find  the values of x and  y.

14.       If sin (A - B)= 2  , cos (A+B)= 2  and  0 <A+B<90° and  A >B then  find the values of A and  B

15.       In a right  angled triangle if hypotenuse is 20 cm and  the ratio  of other  two  sides  is 4 : 3, find the sides.

OR

In an isosceles triangle ABC if AB=AC=13 cm and  the altitude from A on BC is 5 cm.  Find BC

16.       In figure  5,  DE ||AC and  DF ||AE.   Prove  that EF/BF = EC /BE  

17.       The following distribution gives the production of wheat in 100 farms  of a village  per hectare :

Production (kg/ha)        50-55     55-60     60-65     65-70     70-75

No. of Farms                     10           12           24           38           16

Write  the above  distribution as less than  type  cumulative frequency distribution.

18.       Find  the mode  of the following distribution of marks  obtained by 60 students.

Marks Obtained       0-10        10-20       20-30       30-40       40-50

No. of Students           6               5              12             22             15

SECTION - C

Question numbers 19 to 28 carry  3 marks each.

19.       Show that any positive odd  integer is of the form 6q+1 or 6q+3 where q is a positive integer.

21.  Four years ago a father  was six times as old as his son. Ten years later, the father  will be two and  a half times  as old as his son.   Determine the present age of father  and  his son.

OR

Find  a fraction, that  becomes1/2   when 2 is added to its numerator and  while  1 is subtracted from  its denominator it remains 1/3 .

22.       If α  , β  are  zeroes  of the  polynomial x² —2x—8, then  form  a quadratic polynomial whose zeroes  are      2 α  and  2β  .

23.       Prove  that  sec A  (1—sin A ) (sec A +tan A) =1.

24.       If sec A = x + 1/4 x  then  prove  that  sec A+ tan A =2x or 1/2x

25.       In figure   6, OA.OB=OC.OD.   Show  that  

26.       The diagonals of a trapezium ABCD, in which  AB || DC, intersect at O.   If AB =2CD, then find  the ratio  of areas  of triangles AOB and  COD.

OR

In a triangle ABC, the mid  points of sides  AB, BC and  CA are D,E and  F respectively.  Find the ratio  of areas  of triangles DEF and  ∆ABC.

27.       Find  mean  of the following frequency distribution using  step  deviation method.

Classes                0-10        10-20       20-30       30-40       40-50

Frequency              7              10             15              8              10

OR

The mean  of the following frequency distribution is 54.  Find  the value  of p :

Classes                  0-20        20-40       40-60       60-80      80-100

Frequency               7               p              10               9              13

28.       Find  the median of the following data.

Classes            100-150   150-200   200-250   250-300   300-350

Frequency              22             18             25             20             15

SECTION - D

Question numbers 29 to 34 carry  4 marks each.

30.       Prove  that  if a line is drawn parallel to one  side  of a triangle to intersect the  other  sides  in distinct points, the other  two  sides  are divided in the same  ratio.

OR

Prove  that in a triangle if the square of one side is equal  to the sum of the squares of the other two sides  then  the angles  opposite to the first side is a right  angle.

31.       If sec A —tan A =4 then prove that cos A= 8 /17 

OR
      Find the value of sin² 5°+sin²10°+sin²80°+sin²85° 

32.       Prove  that

(1+secA) /sec A =  sin²A / (1—cosA)

33.       Solve graphically :

 x –  y +1= 0,  3x +2y =12

(i)      Find  the solution from  the graph.

(ii)     Shade  the triangular region  formed by the lines  and  the  x—axis.

34.       The following distribution gives  the daily  income  of 50 workers of a factory.

Daily income (in rupees)      100-120      120-140      140-160      160-180      180-200

Number of Workers                    12                14                 8                  6                 10

Change the above distribution to more  than  type distribution and  draw its ogive.